脑洞大师挑战：第25关揭秘，如何以最少刀数将圆均分为八等份？

当提及“脑洞大师挑战”，想必许多人的目光都会被那些富有创意与逻辑的所吸引。第25关——“如何以最少刀数将圆均分为八等份”——就是这样一道激发智力与想象力的题目。这个不仅考验我们的空间想象能力，还考验我们逻辑推理的能力。本文将带领读者走进这个挑战，一起探寻背后的数学原理与几何智慧。

挑战背景

在几何学中，将圆形均分是一个经典。而将圆均分为八等份，更是对分割技巧的一个考验。传统的等分方法往往需要复杂的计算与精确的测量，但在这一挑战中，我们需要在有限的刀数内找到最简洁的分割方式。这个引发了众多数学爱好者和几何学者的兴趣，成为了一个值得深入研究的课题。

挑战详解

一、初始分析与初步尝试

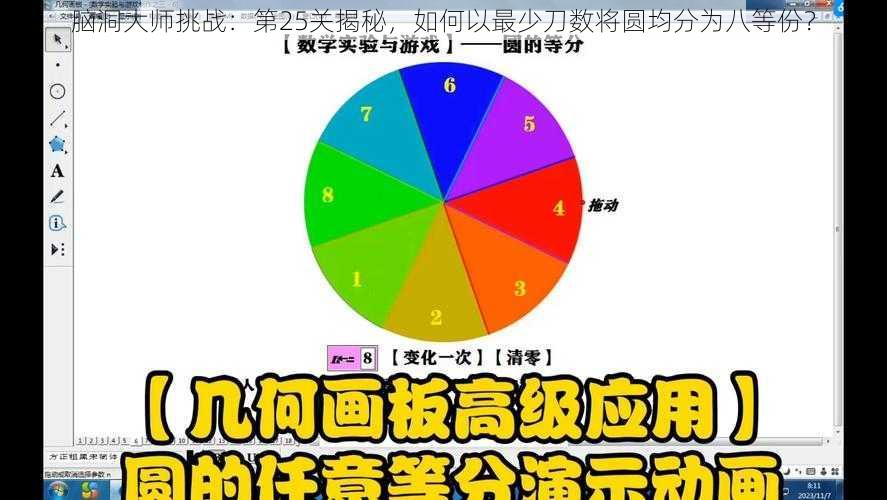
面对这个挑战，我们首先需要理解圆形均分的基础概念。一种直观的方法是通过对直径进行多次切割来完成八等份的分割。但这种方法显然不是最优解，因为它需要的刀数较多。我们需要寻找一种更为高效的切割方法。可以考虑从圆的周边入手，通过连接圆心和圆上某一点，再找到其他关键点进行切割。

二、寻找关键切割点

为了最小化刀数，我们需要找到圆上特定的点，使得通过这些点的连线能够将圆最简洁地分割。通过观察和实践，我们可以发现，通过连接圆心与圆上两个对称的点，再在这两个连线段的中点处进行切割，可以达到八等份的分割效果。这种方法仅需三刀即可完成分割。第一刀连接圆心和圆上的一个点，第二刀连接圆心与第一刀在圆上的另一个交点，第三刀则是经过前两刀交点且垂直于圆心的直线切割。

三、验证与深化理解

为了验证这种方法的正确性，我们可以通过简单的纸笔实验或计算机模拟来验证这一策略。通过实践，我们会发现这种方法确实可行。为了进一步理解这一，我们还可以深入探究平面几何中关于圆和线段的性质，以及如何通过最少的线条划分一个区域的。这有助于我们更加深入地理解这一挑战背后的数学原理。

结论与

通过以上的分析与实践，我们找到了以最少刀数将圆均分为八等份的方法。这一的解决不仅锻炼了我们的逻辑思维能力，还让我们领略了几何学的魅力。在实际生活中，这种分割方法可能并不常见，但它所体现出的数学原理与思维方式却具有广泛的应用价值。对于未来的研究，我们可以进一步探讨如何将这种思维方式应用于更复杂的几何中，或者寻找其他类似的益智，继续锻炼我们的脑力。